The quantum computing revolution is getting closer, but the need for error-correctable computers continues to hold it back.
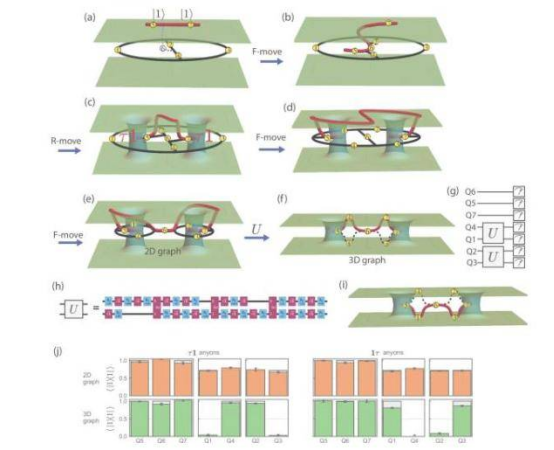
Through a collaboration led by Cornell University with IBM, researchers have taken a major step forward, achieving two significant breakthroughs. First, they demonstrated error-resistant implementations of universal quantum gates—the fundamental building blocks of quantum computing. Second, they showcased the powerful capability of topological quantum computers in solving problems intractable for classical computers.
In a paper published in Nature Communications titled "Realizing String-Net Condensation: Fibonacci Anyon Braiding for Universal Gates and Sampling Chromatic Polynomials," researchers from IBM, Cornell University, Harvard University, and the Weizmann Institute of Science conducted an international collaboration that, for the first time, demonstrated the ability to encode information by braiding (moving in a specific sequence in 2D space) Fibonacci string-net condensed (Fib SNC) anyons—exotic quasiparticles.
"This is effectively the first step toward universal topological quantum computing or fault-tolerant computing," said co-corresponding author Eun-Ah Kim, the Hans A. Bethe Professor of Physics in the College of Arts and Sciences.
"Two-dimensionality is crucial for improving fault tolerance and resistance to errors. If everything is only in one dimension, fault tolerance cannot be achieved," said co-corresponding author Chao-Ming Jian, Assistant Professor of Physics (A&S).
The researchers demonstrated the power of their method on a known hard problem (not one invented for the experiment). On a small scale, they could verify the quantum computer's results with a classical computer as a proof of principle.
The chosen problem involved chromatic polynomials, which arise from counting problems on graphs with differently colored nodes and simple rules. Classical computers can calculate the number of valid colorings for a simple graph with few nodes and colors. But as the graph grows large with many nodes and connections, the number of possibilities explodes exponentially—beyond what classical computers can compute.
The protocol the researchers used—sampling chromatic polynomials for a set of graphs where the number of colors is the golden ratio—is scalable, so other researchers with quantum computers can replicate it on larger scales.
"Someone can follow our recipe and do something that was traditionally impossible," Kim said. "We're throwing down the gauntlet to anyone."
Studying topologically ordered many-body quantum systems (systems of many interacting quantum particles) and their applications in quantum computing is a tremendous challenge for quantum researchers. Kim said that being able to leverage resources, expertise, and insights from scientists worldwide—including both industry and academia—was crucial to their team's success.
She added: "The IBM researchers played a critical role in understanding the theory of topological states and designing protocols to realize that theory on quantum computers—which they themselves develop. Our other collaborators made important contributions in hardware simulation, bridging theory and experiment and validating our strategy."